Abstract
- A special type of Relation where each input value maps to exactly one output value. In relation, we can have one element is a parent of one or more other elements. But in function, we have one element is a square of another element
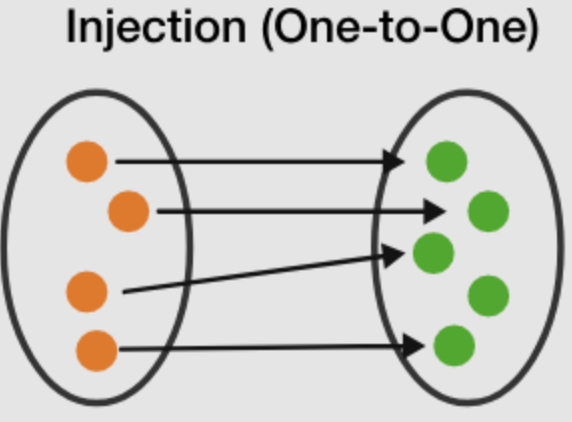
Injective
Each element in the Domain maps to a distinct element in the Co-domain.
Surjective
Every element in the codomain is covered by the function. However, the function shown in the diagram below isn’t injective, since 2 inputs point to the same output.
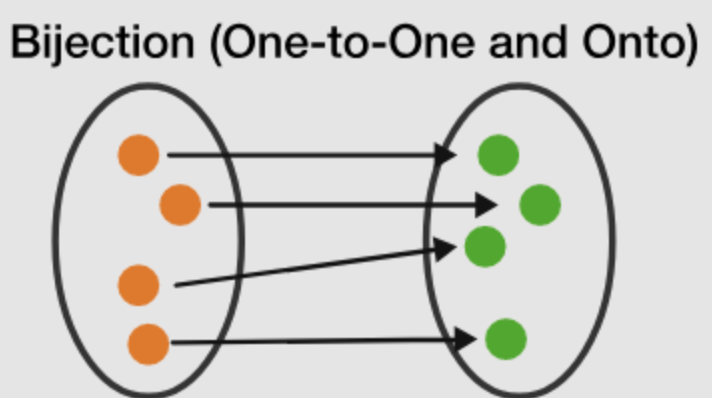
Bijective
When a function is both injective & surjective. When a function has a Inverse Function, we can say it is bijective. Since inverse function uses the codomain of the original function as domain - surjective & inverse function follows the rule of function, each input maps to exactly one output - this shows no input value from the original function maps to more than one output, thus injective.
Purity
The same input always produces the same output.
Referential Transparency
The output depends only on the input.
Inverse Function
- A Mathematical Function that essentially undoes the action of the original function
Example
Given , then .
If , then , .
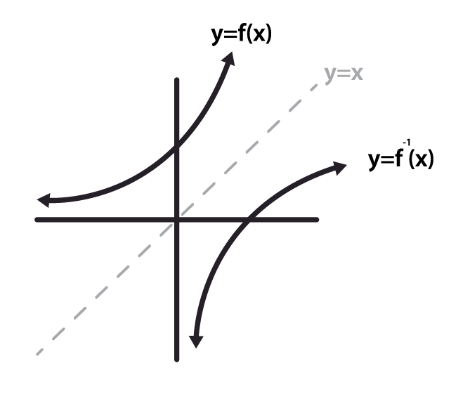
Visual relationship with function
Inverse function is basically a reflection of the original function about the line
Real-value function
- A Mathematical Function that assigns Real Number as outputs for real numbers as inputs. In other words, it’s a function where both the Domain and the Co-domain are Subset of the real numbers
Polynomial Function
- is constant, and the polynomial function above is called polynomial of degree
Attention
A polynomial of degree can be factored as a product of linear and quadratic Factor.
For example, , where and are linear factors and is quadratic factor.
Rational Function
- Both and are Polynomial Function
- The Domain of consists of all Real Number except the root of - the value of that will make